Elliptic Curve Cryptography - Multiple Signatures

• Communications
• Applied Math
• Algorithms

Quick Links

• Part 1: New book on Elliptic Curve Cryptography
• Part 2: Elliptic Curve Cryptography - Basic Math
• Part 3: Elliptic Curve Cryptography - Security Considerations
• Part 4: Elliptic Curve Cryptography - Key Exchange and Signatures
• Part 5: Elliptic Curve Cryptography - Extension Fields
• Part 6: Elliptic Curve Cryptography - Multiple Signatures

The use of point pairing becomes very useful when many people are required to sign one document. This is typical in a contract situation when several people are agreeing to a set of requirements. If we used the method described in the blog on signatures, each person would sign the document, and then the verification process would require checking every single signature. By using pairings, only one check needs to be performed. The only requirement is the ability to verify the public keys of the signers.

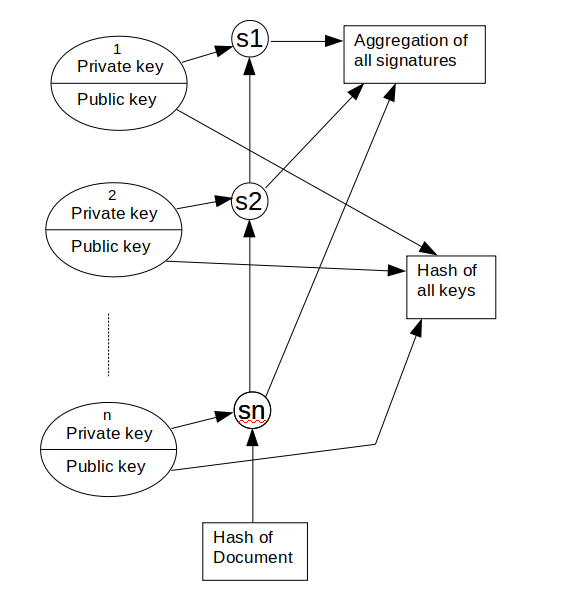
Here is a general view of the process. There are $n$ people who are going to sign a document. The signature acts on the hash of the document, so the choice of hash function and insurance that the document does not change when transferred are essential. Each person has a private key which no one knows and a public key which everyone has access to.

The document is still signed individually by each person. The signatures are then combined mathematically into a single value. The main trick is the combination of all the public keys into a single value. The public keys can be attached to the document for verification, and it should be possible to check that each public key came from the correct person. It is designed so that anyone attempting to falsify the signature by removing or adding another key will cause a verification failure. The final signature consists of one point on the prime field curve and one point on the extension field curve. The aggregation of all the signatures is on the prime field and the hash of all the keys is over the extension field. 

The aggregation process can be performed by one person, or by everyone if nobody trusts anyone else. If the results are not all exactly the same, somebody is trying to break the system. This level of mistrust is ignored, I'm going to assume there is one person that aggregates the signatures and the public keys.

The first mathematical step is to convert the field extension public keys into a string of contiguous bytes in $(x, y)$ order. Call this set of points the string $\{P_1, P_2, P_3, \cdots , P_n\}$. For a 256 bit field, the extension will have about 850 bytes per point so the string could be several kilobytes long for just a few people signing. For every person in the list, the value $$a_j = H_1(P_j, \{P_1, P_2, P_3, \cdots , P_n\})$$is computed. The $j^{th}$ person's public key is used twice - once at the start of the string and once in the list.

The $H_1(\cdot)$ hash function outputs a prime field element, not an extension field element. This is used as a multiplier to create the aggregate of all public keys using the formula $$A = \sum_{j=1}^n {a_j P_j}.$$

This binding of the keys is very interesting. The coefficient depends on all the keys being in the proper order in the list as well as being the correct keys in the signature. And the final point $A$ is on the field extension curve with all the public key points. Any one who has access to the public keys and their order in the hash can recompute the point $A$. Anyone attempting to change the signature by replacing a public key will get a completely different point.

Each person's public key is computed using $$P_j = p_j g_2$$ where the point $g_2$ is on the extension field curve.The point $g_2$ is common to everyone. The signature each person computes uses their private key $p_j$ and the $a_j$ associated with their public key. Because the $a_j$ require the list of public keys, a signing operation can not be done without knowing everyone's public key. And the order of keys matters, so that choice must be defined as well before the signing operation takes place. This binds each individual signature with all the public keys of everyone signing the document.

The signing formula each person computes is $$s_j = a_j p_j H_0(m)$$where $H_0(m)$ is the message hashed down to a point. The point $H_0(m)$ is on the base field curve ($G_1$). The point $A$ is on the extension field ($G_2$). See chapter 18 in Elliptic Curve Cryptography for Developers for details.

The aggregation of the signatures is a simple sum of all the points $$S = \sum_{i=1}^n s_i.$$and the complete signature is the pair of points $(S, A)$. To verify that all the signers did in fact sign the same document, the computation of two parings are compared$$e_m(S, g_2) \stackrel{?}{=} e_m(H_0(m), A)$$where $e_m(\cdot , \cdot)$ is an elliptic curve pairing operation, $S$ is the aggregate sum of signatures, $g_2$ is the common point to all public keys, $H_0(m)$ is a hash of the message to a point, and $A$ is the aggregation of all the public keys.

The point of the verification is that only one comparison is required to check that document "m" was actually signed by $n$ people. To see how this works mathematically we can break down the pairing calculation. Putting $A = \sum_{j=1}^n {a_j P_j} = \sum_{j=1}^n{a_j p_j g_2}$ on the right side and $S = \sum_{i=1}^n s_i = \sum_{i=1}^n {a_i p_i H_0(m)}$ on the left we have 

$$e_m\left(\sum_{i=1}^n {a_i p_i H_0(m)}, g_2\right) \stackrel{?}{=} e_m\left(H_0(m), \sum_{j=1}^n {a_j p_j g_2}\right).$$

On the left we have $H_0(m)$ common to all the terms in the sum. On the right we have $g_2$ common to all the terms in that sum. So we can write this as

$$e_m\left(H_0(m)\sum_{i=1}^n {a_i p_i }, g_2\right) \stackrel{?}{=} e_m\left(H_0(m), g_2\sum_{j=1}^n {a_j p_j}\right).$$

Using the rules of elliptic curve point pairing mathematics, the factors multiplying points become exponents of the pairing. The result is $$ e_m\left(H_0(m), g_2 \right)^{\sum_{i=1}^n a_i p_i} = e_m\left(H_0(m), g_2 \right)^{\sum_{j=1}^n a_j p_j}. $$

The math works out as long as nothing changes. The order of the public keys used in creating the values $a_j$ matter as much as the public keys used in the multiple signature. Once all that is defined, the message itself can not change either or the verification will not match what was actually signed. The private keys remain unknown. The computation of the message hash with the aggregate keys $e_m(H_0(m), A)$ simply has to match the computation of the signatures with the common point $e_m(S, g_2).$ The private keys are hidden by the elliptic curve discrete log problem.

Cryptography is not security. Creating a system which uses this math requires a lot of attention to detail. A system should verify all public keys are sufficiently random - that means you can not know what the private key was that created a public key. The system should ensure only those who are allowed to sign actually do sign - and not someone hacking into the system who should not be there. If everyone is in the same room at the same time using a computer not connected to anything that's pretty easy. Otherwise, it's harder than it sounds.

There are also protocols for one person signing multiple documents and using one verify. Check out BBS multi-signatures to see how that works. To see how this math converts to code, check out the repository Elliptic curve pairings.

Sign in