I’ve been wasting far too much of my free time lately on this stupid addicting game called the Kittens Game. It starts so innocently. You are a kitten in a catnip forest. Gather catnip.
And you click on Gather catnip and off you go. Soon you’re hunting unicorns and building Huts and studying Mathematics and Theology and so on. AND IT’S JUST A TEXT GAME! HTML and Javascript, that’s it, no pictures. It’s an example of an incremental game, also known as an idle game, where you click on this thing and then that thing and wait for your resources to increase and unlock new mechanisms one after the other.

FarmVille (which I have no intention of ever playing) and Cookie Clicker (which I have played and quickly tired of) are also examples. These games make their popularity through a consistent level of novelty, and the illusion that you can somehow speed things up by ushering them on through clicks here or there. SimCity was sort of in this category. I remember playing it in the early 1990’s one evening while home on winter break; it was intriguing, and then when I looked at the time, it was two o’clock in the morning, and I knew I had to burn out my desire to play as quickly as possible and get on with my life.

These games tend to be exponential in nature: if, for example, it takes 200 experience points (or dollars, or catpower, or whatever) to go from level 1 to level 10, it might take another 200 experience points just to get to level 11 and another 400 experience points to get to level 12. If you just keep clicking, you can get there, but it will take essentially forever. But if you unlock upgrades, you can increase the rate of progress, at least for a little while, and keep pace with the whole exponential thing. So the unlocking-upgrades thing is a necessary part of the game for it to remain interesting. Perpetual novelty. Our brains just aren’t wired to like linear progress, I guess. Cookie Clicker soon gets to the point where you are making thousands and millions and billions of cookies per second; it’s kind of silly. I just reopened Cookie Clicker for a moment and it says I have 12.608 quadrillion cookies. Ho hum. You really get to learn the ‑illions on some of these games — which gives me a flashback to being a 7-year-old looking through the Random House Unabridged Dictionary (about the size of a large shoebox and the weight of a bowling ball) and wondering why billion and trillion meant different things in the USA and in England. Centillion = 10303 in the USA, but 10600 in England. I don’t know whether AdVenture Capitalist gets up to one centillion — I haven’t played, but I’ve seen ads for it with screens showing unquadragintillion = 10126. I lose interest just considering it. And I thought inflation in Zimbabwe was bad.

Kittens Game is able to beat the inflation problem, for the most part, through a clever series of upgrade interdependencies; you have to add a few more buildings zooming up exponentially until you run out of resources, but that lets you do something else just a little bit easier, and then upgrade a different thing, and so on, and you can play for maybe a week and still only have 70 or 80 kittens and a few hundred thousand units of wood and minerals. So no need to look up names for insane powers of 10.
The sad part about idle games (whether hyperinflationary or not) is that although they’re meant to be played while you’re doing something else — you check them every once in a while, when you take a break from writing a report — instead they can lure you in, insidiously, to spend more effort so you can progress faster. Instead of just waiting for an hour and coming back later, you can click on this and upgrade that and buy one more widget and so on, until it’s two o’clock in the morning. So I’m working on burning out my interest in the Kittens Game.
But that’s not what this article is about.

Amdahl’s Law and Parallel Processing
In November 2015 I posted an article on Chandrupatla’s method for root-finding, and I got a comment from one reader wishing I had talked about the importance of Amdahl’s Law and its dismal, pessimistic implications, in the context of optimizing algorithms to run faster. (In an eerie coincidence, this comment was posted one day after Gene Amdahl passed away and one day before the notice of his death was published.) Which I thought was odd. If you’re interested in reading about the details of some specific algorithm, you should know something already about the motives and tradeoffs of optimization. An addition to discuss Amdahl’s Law… Relevant? Yes. Appropriate? No. If I watch a TV cooking show covering caramelization and the Maillard reaction, I would neither expect nor appreciate a lecture on the dangers of obesity and excess blood sugar. And yet it’s relevant, and should be given its own time in the spotlight.
So here we are with Amdahl’s Law:
Let’s say you have some tasks that you want to speed up. For example, suppose you have to construct a Pasta House building that takes 10 wooden beams and 10 stone slabs, and you have two kittens, each of which can craft 1 beam per minute as a woodcutter, or 2 slabs per minute as a miner. (That’s not the way it works in the Kittens Game, but never mind, this is just a thought experiment.) Then it’s going to take you 7.5 minutes total if both kittens are operating at peak capacity: the job is 15 kitten-minutes total — 10 kitten-minutes for the beams and 5 kitten-minutes for the slabs — which, for example, we could achieve by having one kitten crafting beams and the other crafting slabs for five minutes, giving us 5 beams and 10 slabs, and then switching both kittens to woodcutter for the next two-and-a-half minutes, giving us another 5 beams.
Then you discover an upgrade for miners that increases the rate of slab crafting, with larger increases the more manuscripts you have; there are no upgrades for woodcutters at the moment. How much faster can you get the materials for this building?
Amdahl’s Law is one way of calculating this. It can be written in a number of ways; one of them is
$${\rm speedup}\ s(f,N) = \frac{1}{\frac{f}{N} + (1-f)}$$
where \( f \) is the fraction of work that can be sped up and \( N \) is the speedup factor of that work. In Amdahl’s original statement, it was in the context of parallel processing; \( N \) was the number of processors and \( f \) was the fraction of work that could be parallelized, with \( 1-f \) being the rest of the work stuck as sequential effort. But it’s really the same issue in almost any logistical context, whether it’s about parallel computing, or the rate at which fast-food workers can finish orders of French fries and hamburgers and milkshakes, or kittens crafting beams and slabs.
In simple terms, Amdahl’s Law will tell you how much faster you can execute an entire set of work, if you can speed up only part of it. You need to use caution, however, in interpreting the result. Amdahl’s Law can help you be more realistic about the effects of performance improvements, but I claim it can also lead you to overly pessimistic conclusions, which I will demonstrate in this article.
Okay, well, let’s plug in the numbers from our Pasta House example. The beams take 10 kitten-minutes and the slabs take 5 kitten-minutes, so \( f = \frac{1}{3} \): the slabs take 1/3 of the total work.
$$s(f,N) = \frac{1}{\frac{1}{3N} + \frac{2}{3}}$$
What happens if we have a 10% upgrade? Then \( N = 1.1 \) and the speedup is a factor of 33/32 = 1.03125 or 3.12%. We can finish the job in 7.27 minutes.
How about a 100% upgrade? Then \( N = 2 \) and the speedup is a factor of 1.2 or 20%; we can finish in 6.25 minutes. Huh.
What happens if we have to leave in four and a half minutes? Can we finish in time?
Zebras hate you for no reason
A 900% upgrade? Then \( N = 10 \) and the speedup is a factor of 10/7 = 1.4285 or 42.85%. Yikes, even if we spend thousands of manuscripts to make the miner kitten faster by a factor of 10, we’ll only decrease our total time from 7.5 minutes to 5.25 minutes. That’s depressing.
Or, restated in a more practical context, let’s say I have a computer program that contains a lot of number-crunching, and it uses some numerical algorithm like Chandrupatla’s Method and I find a way to speed up the number-crunching (whether by finding a better algorithm, or by improving the implementation) by a factor of 10. If it used to take 1/3 of the total program time to execute, then the overall speedup is only 42.85%.
A more likely scenario in software engineering is that I might be able to speed up some aspect of my software by a factor of 1.5 (rather than a factor of ten), so it only takes 2/3 of the time it used to, and maybe before the speedup it comprised 1/8 of the software’s execution time. Then I’m down to \( 1 / (0.125/1.5 + 0.875) = 24/23 \approx 1.043 \). How sad. We sped up part of our code by 50%, a very noticeable improvement, but the overall speed has only increased by about 4.3%. Below is an illustration of this; we’ve sped up task 5, but the overall speed hasn’t changed much:

So why bother?
Well, I can think of several reasons, some of which I’ll be discussing today, and others which I’ll leave to an upcoming article.
First, let’s take a little side trip back to the Kittens Game. At some point in the game, you unlock the ability to trade with other races of beings: there’s the Lizards, who will take minerals from you, and give you wood in return, and the Sharks, who will take iron and give you catnip. (Sharks are useful if you’re desperately low on catnip and want to avoid starvation.) Trading costs some gold (and “catpower” to send a trading caravan) to seal the deal, so it’s not free, but it’s an important path to getting needed resources, including spice and blueprints, which sometimes your trading parters throw into the bargain, perhaps to compensate for the gold, or perhaps because they just feel pity for your general cattiness. Griffins will give you iron if you give them wood in return, and Nagas will give you minerals if you give them ivory.
And then there’s the Zebras.
One of the resources you need to get in this game is titanium. It is used for a lot of things, like the Geodesy skill, which lets your geologist cats find gold directly, rather than having to rely on smelters to produce it in small quantities, and creating units of alloy metal, which are used for all sorts of advanced upgrades.
You need titanium.
There are three ways to get titanium.
One is to trade with the Zebras, who will take stone slabs from you (along with some hard-won gold), and in return they will give you iron, and possibly throw in some metal plates and titanium. Who knows why Zebras have an innate ability to produce titanium… they just do. But the Zebras are hostile, and there’s a 30% chance that they’ll take your slabs and gold and give you nothing, with just a note in your log:
- Your kittens return empty-pawed
- You have sent 1 trade caravan
- Zebras hate you for no reason

It’s a real bummer to rely on the Zebras.
The second method of obtaining titanium is to build a calciner, which converts minerals into iron and a small amount of titanium, using up some oil in the process. This is one way of getting continuous production of titanium, without any direction on your part. But calciners are hard to build. You need to save up enough science to unlock the Chemistry upgrade; calciners aren’t even visible until you do that. And then you need steel and blueprints and oil… and some titanium to start with.
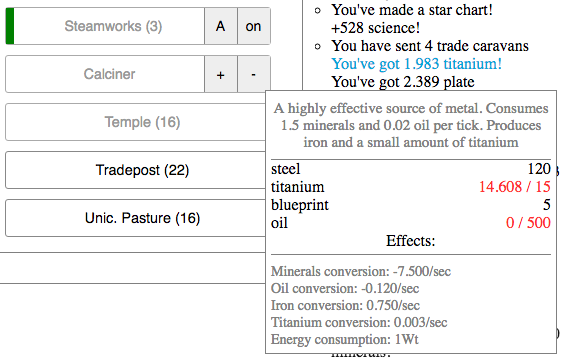
The third method of obtaining titanium is via the wood-burning smelters that convert minerals into iron and coal and a little bit of gold. If you unlock the Nuclear Smelters upgrade, the smelters will also produce a little bit of titanium. But to do that, you need quite a bit of uranium, and that comes much later in the game.
So you need the Zebras after all. You have to save up enough gold to trade and trade and trade with the Zebras until you finally have enough titanium to build a calciner and you can make titanium on your own, freeing you from their rutile monopoly. Although it turns out that later in the game, your trading ability improves, and Zebras really are the easiest way to get a whole bunch of titanium when you need it; you just have to factor in some loss of titanium, because, after all, they hate you for no reason.
Zebras revisited: Amdahl’s Law isn’t so black and white
So what do the Zebras in a stupid idle game have to do with Amdahl’s Law? Let’s look at that picture of the task speedup again:

There are some insights we can draw from this.
First and foremost, Amdahl’s Law has some analogs with the idea of efficiency, which I pointed out a few years ago in another article on that subject. Basically it boils down to the idea that looking at efficiency is a way of treating the idea in relative terms, and in some cases what really matters is absolute terms. Yes, we had to work hard to speed up task number 5, and maybe we only saved 2 1/2 minutes out of an hour’s worth of computation, but we did get some speedup. The remaining tasks could take an hour, or a day, or a month, and that wouldn’t change the fact that we put in X amount of effort and got a 2 1/2 minute speedup each time our whole set of tasks is complete. (Whether or not that speedup is worth it, is another question, and I’ll be talking about this in another article.)
The second insight has to do with an aspect of efficiency that comes up in thermodynamics, namely Carnot’s Theorem, which puts bounds on the efficiency of a heat engine, based on the absolute temperatures involved. Let’s say you have an steam engine with internal temperature of \( T_H = 200^{\circ} \text{C} = 473 \text{K} \), and a coolant reservoir that is at \( T_C = 40^{\circ} \text{C} = 313 \text{K} \) — its maximum efficiency from fuel to useful work is \( (T_H - T_C) / T_H = 33.8\% \), but most likely it’s less than that. The brutal fact is that heat pumps and air conditioners and refrigerators have physical limits on efficiency based on their working temperatures, and you can’t do any better than that. Gasoline burnt in a car isn’t going to be able to deliver all of the energy content into physical motion, because of the cap on thermodynamic efficiency. Tough luck. And a common paraphrasing of the three Laws of Thermodynamics, sometimes attributed to C.P. Snow and sometimes to Allen Ginsberg, applies here:
- You can’t win
- You can’t break even
- You can’t quit the game
You just can’t get around being inefficient; yep, Amdahl’s Law applies, you lose, them’s the breaks. Zebras hate you for no reason. When you plan on speeding up part of a series of logistical tasks, you should know what you’re getting into.
The third insight is that if we want to speed up a series of tasks, most likely we’re not only going to put our efforts into just one task, but rather we’re going to look at them all, and hopefully we can get this kind of speedup illustration

where we work hard, and get many of the tasks (not just one) to be more efficient, so that our overall process can work faster. If task 5 is the hardest one to speed up and we focus effort first on the remaining tasks, then the results may look like this

and by virtue of Amdahl’s Law, the tasks which are the bottlenecks (task 5 here being a prime example) are, in fact, the ones that have the most attractive return on investment when we haven’t done them yet. ROI is something about which I’m going to skip over any discussion today, but keep it in mind.
The fourth insight is that even if we don’t get much of a gain from only speeding up one of many tasks

it still might be valuable. In many industries, slight advantages still have a lot of leverage in the marketplace. If Netflix charges \$9.99 a month for streaming video, and some new Company X charges \$8.99 a month for essentially the same content, I’m going to switch to Company X. It’s not much of a savings, but why throw away money unnecessarily? Being the least expensive or highest performance in the industry, even by a little bit better, can command a premium share. Even if that’s not the case, there are industries, like retail, which operate on very small margins, so a savings of 1% in costs of goods and services (COGS) is a large amount relative to their net profit margin: if my revenues are \$100 million, COGS are \$60 million, and my net profit (after paying all the other expenses like salaries and rent and health insurance) is \$1 million, a savings of only 1% in COGS will increase net profit by 60%, to \$1.6 million. These industries with small margins try to shave off every possible cent in order to keep their bottom line profitable, and in the process they can make a difference between having a bright future and going bankrupt.
Gustafson’s Law
Let’s go back to our Pasta House thought experiment.
Just to remind you, a Pasta House building takes 10 wooden beams and 10 stone slabs, and you have two kittens which can act as woodcutters (crafting 1 beam per minute each) or as miners (2 slabs per minute each); the job will take 7.5 minutes total: 5 minutes for beams and 2.5 minutes for slabs.
Let’s suppose we unlock a speedup for the miners so they can now craft ten times faster, or 20 slabs per minute. The job will take 5 minutes for beams and 15 seconds for slabs, for a total of 5.25 minutes, or a speedup of 7.5/5.25 = 1.4286 — that’s 42.86% faster.
As we calculated earlier, Amdahl’s Law predicts this: \( s(N,f) = 1/(f/N + 1-f) \) for \( N=10 \) and \( f=1/3 \) will yield \( s(N,f) = 10/7 \approx 1.4286 \).
But maybe I’m not in such a hurry. Maybe I have 7.5 minutes anyway; I budgeted that much time before I found out about this magnificent mining upgrade. And I look at my miner cats and think to myself, Gee, I can create lots of slabs… maybe I can do something else with the slabs.... It takes me 5 minutes for 10 beams, and with the other 2.5 minutes I get 100 slabs… wow! I have 90 slabs left over after the Pasta House. Maybe I use the other 90 slabs to trade with the Zebras. Or maybe I decided to build a Stone Mansion instead with 100 slabs and 10 beams, because the Stone Mansion has some better perks than the Pasta House — and besides, I’m on a low-carb diet. Anyway, same total time as before the upgrade, better result.
This is the product of Gustafson’s Law, which basically says that, yeah, you could calculate things according to Amdahl’s Law, and speed up the same set of tasks, but when you find out that you can suddenly do things faster, you get more ambitious, and respecify the problem to make use of the new speedup. There’s an equation here, too, but that’s not the important thing; the important thing is that we say to hell with Amdahl’s Law, it’s mis-applied. For example, if I have a DSL connection at 2Mb/sec, and I download 3 megapixel pictures of Angela Lansbury, and then I upgrade my DSL connection to 20Mb/sec, I’m not going to be satisfied downloading the 3 megapixel pictures in less time; instead, I’ll download the 12 megapixel pictures of Angela Lansbury, which I wouldn’t have done with a 2Mb/sec connection, but now they don’t take so horribly long and I can just click and get instant gratification.

Synergy: One small step for Catkind
The last insight I have to share — and this may be harder to grasp — has to do with the concept of synergy, and technological advance.
Suppose in the Kittens Game I can manufacture stone slabs 10 times faster… but it lets me build Pasta Houses only 42% faster. Disappointing. But because of the increase in Pasta House construction, I might be able to manufacture Carbonara Sauce 42% faster. This, in turn lets me run 42% more Marathons, which gives me 42% more Gold Medals, which I can use to trade with the Crocodiles, who give me Lenses that I can use to unlock the Photography Equipment upgrade, and that makes more Blueprints, which means that I can get the Norm Abrams Dado Jig upgrade, and if I can do that, then I can create wooden beams 25% faster. Now it gets interesting, because we have a feedback loop: we’re up from 2 beams per minute to 2.5 beams per minute, and with the 20 slabs per minute, it now takes only 15 seconds for 10 slabs and 4 minutes for 10 beams, which is a total of 4.25 minutes. We’ve gone from 42% faster to 76% faster. Then after I get enough Carbonara Sauce and Lenses, I can unlock the Cooking Show upgrade, which generates Likes, and that increases my Happiness, which lets my Farmer kittens produce more food, so I can afford to feed more worker kittens, and they can make more stone slabs and beams....
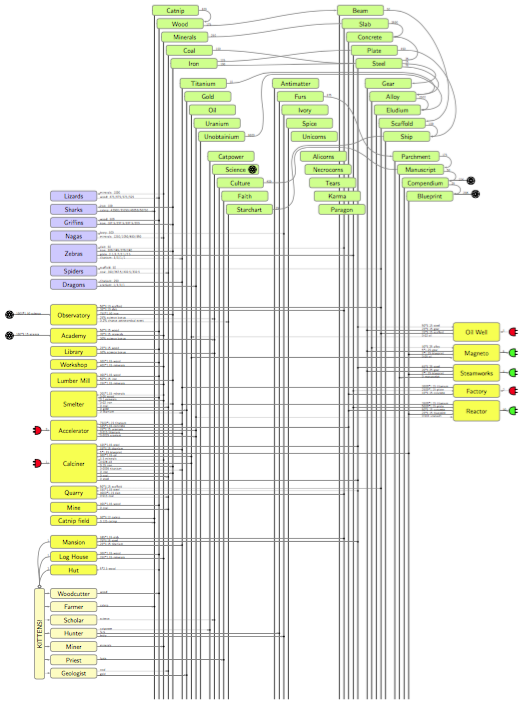
Okay, that example was rather silly, and perhaps hard to follow, and none of those things (except for blueprints and the kittens themselves) are from the Kittens Game, anyway. Let’s look at some of the actual Kittens Game mechanics. I started putting together a chart illustrating this, and quickly realized it was impractical to put everything into a chart, so I’ve shown just a portion of the Kittens Game universe in the chart below. (Still spent way too much time on it.)
A quick tour: the pale tan boxes in the lower left are the various jobs the kittens can perform: Woodcutter, Farmer, Scholar, and so on. The ugly bright yellow boxes are buildings, which fall into several categories. You can increase your kitten population by building various types of housing: Hut, Log House, and Mansion. The other buildings serve different functions, mostly storage or resource processing or power generation, although there are a few weird ones that I didn’t show on the chart, like the Ziggurat, which is used for harvesting unicorn tears. Ahem. Anyway, the green boxes at the top are resources, some of which come directly from buildings or the different kitten jobs, but the rest you have to craft by gathering appropriate combinations of other resources. The periwinkle-colored boxes in the upper left are the other trading civilizations: Lizards, Sharks, Griffins, and so on. Lines with an arrow show resource production or conversion. Lines with a square on the end represent building costs, denoted as something like 5*2.5 which means the first building costs 5 units of the appropriate resource, but it increases by a factor of 2.5 thereafter (5, 12.5, 31.25, etc.). The funny atomic symbol represents Science (just to avoid having more lines crisscrossing the diagram), and the plug symbols represent electric power sources, colored green, and sinks, colored red. Diehard fans of the Kittens Game will remark that this doesn’t include any of the storage buildings, or the Space buildings or missions, or the Science or Workshop upgrades, or any of the parts of the game dealing with religion or Metaphysics, and Engineer kittens aren’t shown… yeah, whatever, let’s see you try fitting them all on a single chart.
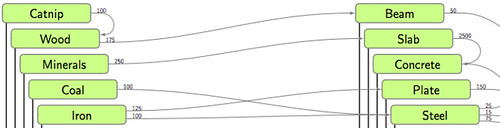
More specific examples might make this clearer. Here’s some of the resources at the top:
There’s an arrow, labeled “100”, connecting Catnip to Wood. This means that if you have 100 units of catnip, you can convert them through the miracle of crafting (“Refine Catnip”) into 1 unit of wood. This is the only crafting you can do at the beginning of the game; later on, you need a workshop, which also gives you a bonus factor of 6% extra for each Workshop. You can convert 175 units of wood into 1 beam, 250 units of minerals into 1 slab, and so on. Some conversions require multiple resources: you need 100 units of coal and 100 units of iron to convert into 1 unit of steel.
Here are some of the buildings:
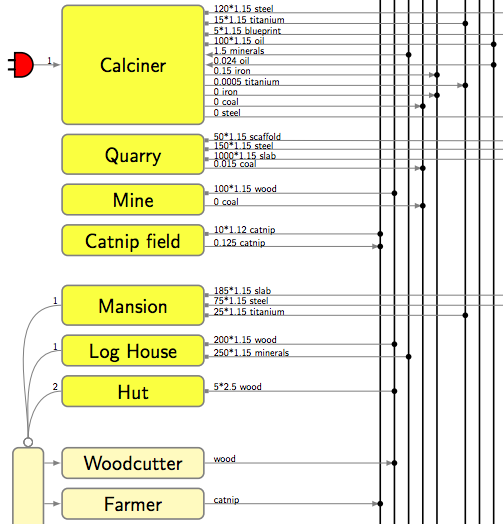
The first catnip field, for example, costs you 10 units of catnip to build, and produces 0.125 unit of catnip per time tick. (There are 5 ticks/second real time, so that’s 0.625 units of catnip per second real time.) The second catnip field costs 12% more, or 11.2 units of catnip. The third catnip field costs 12% more than that, or 12.544 units of catnip. The prices go up exponentially, so that at some point you reach a practical barrier where you can’t really build any more.
Building the first calciner costs 120 steel, 15 titanium, 5 blueprints, and 100 oil. To run it requires 1.5 minerals per tick, 0.024 oil per tick, and 1 watt of power, and it will refine the minerals into 0.15 iron per tick and 0.0005 titanium per tick. (Nifty! A whole titanium factory running on just 1 watt of power.) Initially that’s all a calciner does, but later in the game you can also get calciners to produce steel from iron and coal, which is why they’re labeled with 0 in this chart; the number can increase later, but initially it’s zero. (The iron and coal arrows are going the wrong way, though. Ugh, I knew I would make at least one error.)
Huts can house 2 kittens; Log Houses and Mansions only house 1 kitten each. Funny, how a Hut can hold twice as many kittens as a Mansion, but that’s how it is.
Anyway you get the idea. Read the Kittens Game wiki or play the game if you want complete and accurate information.
Now back to our idea of synergy. The crafting sequence that gets to blueprints is pretty dismal: at the beginning of the game you need
- 175 furs to convert to 1 parchment
- 25 parchments (and 400 culture) to convert to 1 manuscript
- 50 manuscripts (and 10000 science) to convert to 1 compendium
- 25 compendiums (and 25000 science) to convert to 1 blueprint.
This sounds like the St. Ives nursery rhyme; to make 1 blueprint you need over 5.4 million furs, 500,000 culture, and 275,000 science. This takes an incredibly long time and it’s not a good way to make blueprints at the beginning of the game; it’s quicker to trade with Zebras or Lizards, where occasionally they just throw in a blueprint for you.
But each time you buy another workshop, it gets easier; with 1 workshop, your 25 compendiums convert into 1.06 blueprint; with 5 Workshops, your 25 compendiums convert into 1.30 blueprint. (The 6% per workshop is additive.) The real advantage comes with multiple stages of crafting; the benefit of 5 workshops, if you convert from furs to blueprints, is \( 1.30^4 = 2.8561 \), since there are 4 stages of crafting involved. If you can manage to get 25 workshops, that’s a bonus of 150%, so each stage multiplies by 2.5, and you have a crafting gain here of \( 2.5^4 = 39.0625 \); now you only need 350,000 furs (and appropriate amounts of culture and science) which convert to 5000 parchments (since 175 furs now convert to 2.5 parchment), which convert to 500 manuscripts, which convert to 25 compendiums, which convert to 2.5 blueprints.
When you can get blueprints more easily, then it’s easier to make magnetos, and magnetos increase your production rates from other buildings, so you get more wood and minerals and coal and so forth, and that means you can build another workshop, and the cycle just goes round and round. It’s a positive feedback loop! The only things stopping you from zooming up into the quintillion range is the fact that buildings get exponentially more expensive to build, and you have to have enough storage space to store some of the resources. It may take a long time to get there, meaning hundreds or thousands of game years (1 game year = 800 seconds real time), but eventually the production rates get much larger because of these feedback loops.
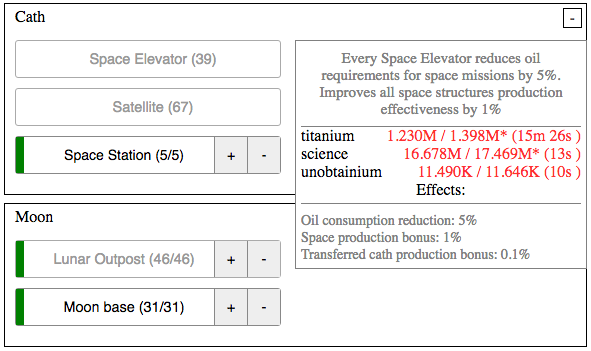
Another aspect of the game that is synergistic has to do with the production multipliers. If you hover over one of the resource rates in parentheses, a window pops up that gives you an analysis of the production and consumption. Here’s an example from a late-stage game of titanium production:

At this time, I have 87 smelters and 19 calciners. At the beginning of the game, the smelters don’t produce any titanium, and when you first build calciners each one produces 0.0005 titanium per tick = 0.0025 titanium per second. There are three upgrades for the calciners (Oxidation, Rotary Kiln, and Fluidized Reactors) which combine additively to increase titanium production by a net factor of 9.1, or 0.02275 titanium per second. When you unlock Nuclear Smelters, the smelters produce 0.0015 titanium per tick = 0.0075 titanium per second. With all those upgrades and 87 smelters and 19 calciners, the total production rate is 1.08475 titanium per second. But wait, we’re not done yet. There are multipliers for Paragon, Magnetos, Reactors, Faith, and Cosmic Microwave Background Radiation that bump it up to about 78 titanium per second. Compare that to what 87 smelters and 19 calciners would provide without any upgrades or bonuses: 19 * 0.0025 = 0.0475 titanium per second from the calciners and none from the smelters. So there’s a net increase of about a factor of 1640! Each of the different improvements combines multiplicatively, and bit by bit by bit the production rate goes up.
What I find interesting about the game is that it caricatures the way technological development happens in the real world. I bought a \$200 Chromebook a few years ago, which contains billions of transistors and a battery and a reasonably nice color display — and to get here has required a huge number of incremental improvements over every piece, some of which would not be possible without previous improvements. For example, today’s processors are designed using computers, and the molds for the plastic parts are surely based on CNC machining, which requires computers, so someone had to design all those computers or their predecessors originally without using a computer, and those computers were very expensive. And all the supply lines are optimized now, so that we can get a laptop computer produced and sent to your house more quickly and conveniently than, for example, a horse; in 1950, on the other hand, procurement and maintenance of the horse would have been much easier and cheaper. Occasionally there are jumps in technology, like the shift from vacuum tubes to transistors, but mostly there are a lot of small tweaks that just make everything a little easier or faster or cheaper. All that technology; if you take a chunk of it away, or if major parts of it fail, all of a sudden it would be next-to-impossible to have smartphones or laptop computers. Or even pencils:
I started reading Thomas S. Kuhn’s The Structure of Scientific Revolutions hoping to gain some insight on this, but found it a little too erudite for my taste; maybe I’ll try again sometime.
Synergy in the Real World: A More Realistic Example, and Why Eeyore and Tigger Can Be Happy Together
So all that stuff about calciners and magnetos and faith combining together to produce boatloads of titanium is kind of silly. Furthermore, the multiple positive feedback loops in the Kittens Game are more representative of macroeconomics and technology development on a worldwide scale over decades, rather than anything you might encounter at a smaller scale. But let’s look at a more practical example of synergy in the real world.
Suppose you and a couple of college buddies decide to start a new company based around the idea of Face Recognition as a Service (FRaaS). Basically you publish a web API that accepts Face Recognition Requests (FRR) containing an image file, and your FRaaS will try to figure out who it is, and respond with a name and Social Security Number. (Great for thieves dabbling in identity theft who don’t have a lot of spare time to work all the details.) You have a prototype working on Orinoco Web Services (OWS), and you’ve estimated, after a lot of careful calculations, that if you scale up the idea, you can charge 1.6 cents per FRR, each of which you can respond to in 1.0 second, and at that cost and performance you can reasonably expect a minimum of 9 million FRRs per month, for a computing cost to you of 0.7 cents each. Total cost: \$63000/month. Total revenue: \$144000/month. Gross profit: \$81000/month. A more likely scenario is a volume in the 20-30 million FRR/month range, but you’re trying to be conservative, at least from the point of view of a business plan.
Here’s the breakdown of the cost per FRR using OWS’s pricing model and some measurements of your software:
- \$4000/month fixed cost (0.044 cent per FRR at 9M FRR/month) based mostly on storage of your software and face recognition database
- 0.05 cent per FRR for the API, covering network traffic and request handlers and so forth — this is what your service would cost per FRR just to send back
200 OKfor each request without any additional processing - 0.45 cent per FRR for the compute time
- \$14000/month cost (0.156 cent per FRR at 9M FRR/month) to reserve peak CPU and RAM loads to service 50 FRRs per second with 1 second response time. Orinoco Web Services makes you do this, even if you don’t actually have any FRRs at all, in order to ensure that the computing power will be available whenever you need it. You don’t need to pay this cost, but then your FRaaS might slow to a crawl if there’s a lot of traffic, and nobody likes a slow FRaaS. Servicing 50 FRRs per second continuously for a month is about 130 million FRRs, way above your expectations, but you want to be able to handle bursts of activity.
Now here’s where it gets interesting. You’ve profiled the computations needed by your algorithms, and it appears that approximately 52% of the compute time is used by one particular function of a Deep Learning software library called Cogitate. Your algorithms call Cogitate’s ponder() method 18 times for each FRR. It looks like there are two improvements you can make:
-
If you change your algorithm to be a little more clever, you can call
ponder()only 6 times per FRR, with only a slight loss in accuracy. -
You can purchase an upgrade to Cogitate that takes advantage of optimized mathematical libraries, and it should reduce the time of each
ponder()call by about 30%.
With both of these improvements, this means you can cut the compute time cost of the ponder() method by a factor of \( 6/18 \times (1-0.3) = 7/30 \approx 0.233 \), or a speedup of \( 30/7 \approx 4.2857 \). This applies to 52% of the compute time. If we plug into Amdahl’s Law, we have \( N = 30/7 \) and \( f = 0.52 \), so the net speedup is \( 1/(f/N + 1-f) \approx 1.663 \), only about 66% faster in multiplicative terms, and only 39.9% faster in relative terms: compute time went down from a baseline of 1 second per FRR to 0.6013 second. We should expect your compute cost per FRR to drop from 0.45 cent to about 0.27 cent.
Again, this is just another way of looking at the compute cost:
- 48% of 0.45 cent = 0.216 cent that won’t be affected by the improvements
- 52% of 0.45 cent = 0.234 cent that will be reduced by a factor of 7/30 to 0.0546 cent, saving us 0.1794 cent per FRR
- total of 0.216 cent + 0.0546 cent = 0.2706 cent
Yay, you can drop your total cost per FRR down to 0.5206 cent, saving almost 0.18 cents per FRR out of the original total of 0.7 cents (0.45 cent for compute cost and 0.25 cent for other factors); that’s about 25.7% cost savings from a factor of 4.29 speedup of part of the program.
Dismal. Depressing. Amdahl’s Law hits us twice as hard, once because ponder() is only part of the program’s computation time, and then again because the computation time is only part of the cost.
But that’s okay, you could live with that inefficiency; making these improvements would raise gross profit to about \$97150/month, which is a little better, and it should reduce the response time by almost 40%, making your customers happier.
When you bring this information to Cameron, your marketing expert, she gets all excited, and plugs in some numbers into her computer, and goes to get a cup of coffee while it churns away at statistical models. A few minutes later she tells you that with the shorter FRR processing time, you can afford to reduce the cost to your customers to 1.2 cents per FRR, and with the increase in performance and the reduced cost, you can conservatively expect 16 million FRR/month rather than the 9 million FRR/month original projection.
Then Dale, your cloud computing expert, tells you that with the shorter processing time and the increased 16 million FRR/month projection, your OWS costs should improve:
- \$4000 per month fixed cost – this doesn’t change, but now that it’s 16M FRR/month, when you divide this cost up, it is only 0.025 cents per FRR
- 0.05 cent per FRR for the API – this doesn’t change
- 0.2706 cent per FRR for the compute time, reduced from 0.45 cent because of the computational speedups
- about \$14800 per month cost to reserve peak loads – the peak FRR rate should increase, but because you cut the processing time down, the peak computational burden is only a little larger than before, and with the increase in reserve, OWS gives you a very slight decrease in pricing. This means your cost to reserve the peak load is down to 0.0925 cents per FRR
Total estimated cost per FRR: about 0.438 cent per FRR. You saved 0.18 cents per FRR from the compute speedup, and another 0.082 cent per FRR from the economies of scale. Synergy at work!
Gross profit would now be 16 million FRR/month × (1.2 cents cost to consumers - 0.438 cent cost to you) = \$121,000 / month! That’s \$40,000 / month more than your original projection! Even if the Cogitate upgrade costs \$50,000, and the work to restructure your algorithm for 6 calls to ponder() has an estimated cost of \$30,000 for all the development and testing, they would pay for themselves in only 2 months.
Furthermore, at these new projections, you can afford to hire another software engineer to try to speed up the other 48% of your compute time, which should drop your FRR costs and response time further, and raise demand and profits.
In summary, for your FRaaS situation:
- Major speedups (4.286×) in a portion of the compute time produced a processing reduction of 39.9%, which is only a portion of the raw cost and yields an even more modest cost reduction (25.7%) because of Amdahl’s Law. Boo. Pessimism.
- Implications of this cost reduction and performance increase lead to improved pricing for consumers which leads to increases in volume, which means more revenue
- Economies of scale reduce other costs besides the reduction in compute time, increasing gross profit
- Preceding increases now allow other opportunities for improvements that were not previously possible
Synergy at work! Amdahl’s Law may mean that you’re stuck with Eeyore when assessing the immediate effects of some performance speedup (namely it won’t help as much as you’d really like), but you shouldn’t neglect Tigger, who really wants you to look at the big picture and see the benefits of positive feedback.

Now, there are some dark aspects here:
The massive improvements we’ve had in technology do allow us to raise productivity and reduce cost, so that you can now get cheap shoes from Amazon.com and Wal-Mart, but now they’re mostly made in China, and many of the large shoe factories in the USA and Europe are gone because they could no longer compete. So if you want shoes made of quality leather that is stitched together for durability, rather than synthetic materials glued together, they’re much more expensive. They’re not only more expensive because the process is more expensive; they’re more expensive because the old way of making shoes is no longer mainstream, and the lower volumes mean that manufacturers are harder to find and have to charge more as a result. Synergistic productivity increases tend to outcompete those methods that fall behind in productivity, even if we would like them to continue. We’re the victims of our own success.
Another big issue is that the sheer complexity and scale of the processes that make this synergy possible also hide some of their impacts to our ecology. Electricity is cheap because we have all these huge power plants that send smoke and CO2 into the sky, or produce nuclear waste, or submerge canyons behind a hydroelectric dam. Palm oil plantations displace tropical forests. Cement quarries in Cambodia are destroying rare limestone cliffs. Mining for coal, gold, copper, silver, and other materials destroy large areas of natural habitat and produce toxic chemicals. Land needed to grow corn, wheat, soybean, and other crops in 2012 consumed more than 52% of total geographic area of the US “Corn Belt” states (Iowa, Missouri, Illinois, Indiana, and Ohio), including more than 80% of the state of Iowa. Add in pastureland and rangeland, and it turns out that agricultural use consumed more than 85% of the total geographic area of the Northern Plains states (North Dakota, South Dakota, Nebraska, and Kansas), with Nebraska topping out at more than 90%. It’s not that all of this is a bad thing, it’s just that there are very large costs in land use to produce all of the electricity, raw materials, and food that we consume as a society… and we just don’t see it because it’s simply not visible unless you go to a power plant, or a dam, or a mine, or a ranch, or a farm. So if I turn on the light or buy copper wire or eat a hamburger, my decision and the decisions of millions of fellow consumers are motivating the business and environmental practices of the power and mining companies and the farmers. Something to think about.
For the most part, though, the consequences of synergy are a good thing.

So What Does This Have to Do with Embedded Systems?
As usual, I find myself drifting onto interesting tangents that don’t have much to do with embedded systems, and since this is a website about embedded systems, I have to search a bit to show that it’s still relevant.
If we’re talking about the fundamental equation of Amdahl’s Law, it still applies to embedded systems just as equally as cloud computing. If you have an interrupt service routine that takes 6400 clock cycles, and you can speed up one part of that from 1800 clock cycles to 400 clock cycles, you’ll cut your total ISR time down to 5000 clock cycles: a speedup of 4.5 in one part translates to a speedup of 1.28 in the whole ISR. Plug the numbers \( N=4.5 \) and \( f=1800/6400=0.28125 \) into Amdahl’s Law and you’ll get the same result.
The moderate or large number-crunching efforts that you run into on desktop PCs or in cloud computing don’t really show up much in embedded systems, though, so the kind of algorithm improvements don’t really happen much, and factors of 5 or 10 speedup are really rare. I would be surprised if I ever ran a root-finding method like Chandrupatla’s Method on a microcontroller… although you never know.
As far as synergy — those effects are present, although you sometimes have to look beyond the embedded systems themselves. For example, let’s say I’m working on some firmware program in C that takes 60 seconds to compile on my computer, and I typically do this compilation step about twenty times a day. That’s 20 minutes, or 4.2% of an 8 hour day. I could buy a faster compiler, or purchase a solid-state drive (SSD) to be faster than a traditional hard disk, and get the compile time down to 5 seconds (factor of 12 speedup!) but it would only save me about 18 minutes each day, and if I had a short-sighted manager he might tell me, sorry, we don’t have the budget, it’s not worth the expense, just do something else while you’re waiting for it to compile. Go browse reddit, it’s okay. Yet a decrease in disruption to a programmer from 60 seconds to 5 seconds is huge! With 60 seconds, I have to stop and wait, and at the end of that 60 seconds I have to regain my train of thought. Whereas with 5 seconds, I can keep my train of thought going and be more productive. Furthermore, since the compile time is smaller, I might compile more often in order to catch syntax errors. Modern IDEs, especially for languages like Java that are faster than C to compile, now have a continuous compilation process that recompiles the file you’re working on whenever it sees a change, and as a result you see a little warning pop up immediately to tell you that you made an error. Instant feedback, and it’s much quicker to avoid little stupid mistakes.
Another aspect of synergy that may affect an embedded systems designer is the consequence of speeding up CPU time. If I can cut my ISR time from 6400 clock cycles to 5000 clock cycles in an embedded system, maybe I can use a slower system clock, saving battery energy and requiring a smaller, less expensive voltage regulator on board, with less heat to dissipate, so heat sinks might cost less. So even if Amdahl’s Law says the immediate result of my speedup isn’t too impressive, there are other multipliers out there that magnify the effects of my improvements.
Wrapup
Okay, so what did we learn today?
-
Amdahl’s Law says that for some set of tasks, if a fraction \( f < 1 \) of them can be completed \( N \) times faster, for whatever reason — new algorithm, faster computer, more kittens — the entire set of tasks will experience a speedup rate of \( \frac{1}{\frac{f}{N} + (1-f)} \), which is always less than \( N \); you get a smaller speedup overall because only part of the work is made faster.
-
Amdahl’s Law essentially tells you there’s an efficiency factor at work that depends on how much of the total task can be sped up. It’s no big deal, as long as you understand this and keep it in perspective, and it may even help guide you towards focusing on improvements that affect a larger portion of the total execution time.
-
For some applications, making even small improvements in productivity is worthwhile, so you shouldn’t necessarily let Amdahl’s Law stop you from making those small improvements just because it says you have to work hard to do so.
-
Gustafson’s Law is another way of looking at the same situation, and deciding to take advantage of the partial speedup, by using the same total time and getting more work done, rather than trying to do the same amount of work in less time
-
Some applications may even experience synergy, where small improvements in productivity are leveraged into larger net value, which can mitigate the otherwise pessimistic implications of Amdahl’s Law.
-
We looked at this in context of the Kittens Game, but it’s applicable to real life, too.
I’ll be following up today’s article with another one on cases when it’s not appropriate to optimize.
But in the meantime, don’t stop seeking improvement! And if you’re playing the Kittens Game… take a break, get up from your computer, go spend time with your family and take a walk outside. You won’t regret it.

p.s. I started writing this article in December 2015, but put it on hold shortly thereafter, while working on the Padé delay article, and managed to free myself from the Kittens Game a month or two later. When I resumed working on this article a few weeks ago, I took some screenshots from the game and double-checked a couple of facts about it. Unfortunately now I’ve been sucked in again....
© 2017 Jason M. Sachs, all rights reserved.